Arc Notation
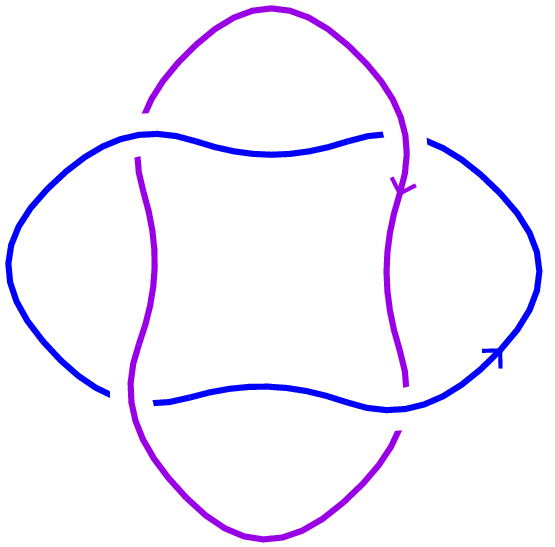
The arc notation for an oriented link is obtained by first describing an arc presentation (or grid diagram) for the link. An arc presentation is a link diagram (in the usual sense) placed on an n×n (x,y)-grid so that for each x-ordinate from 1 to n there is precisely one (oriented) vertical arc, and for each y-ordinate from 1 to n there is precisely one (oriented) horizontal arc. Additionally, it has the property that the vertical arcs overcross the horizontal arcs. See the figure below for an arc presentation of L4a1{0} .
Given an arc presentation for an oriented link, its arc notation is given as follows. Beginning with the horizontal arc at y=1, assign it an ordered pair {a1, b1} if the arc begins at (1,a1) and ends at (1,b2). Repeat for horizontal arcs at y=2, 3, ..., n to obtain an ordered list for ordered pairs. In the example of L4a1{0} below, from the arc presentation we read off: n=6 and {{6,4},{3,5},{4,2},{1,3},{2,6},{5,1}} is its arc notation.
 |
 |
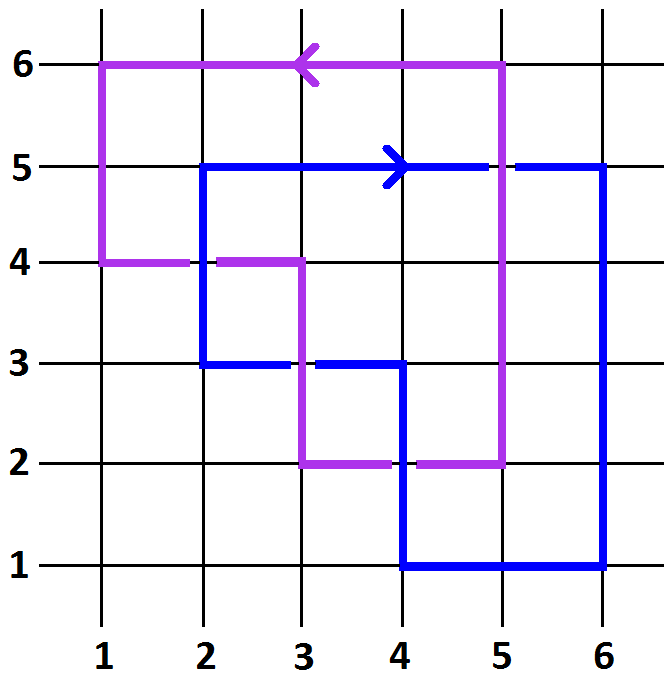 |
| L4a1{0} | Another view of >L4a1{0} | Arc presentation for L4a1{0} |
Remarks
The arc notation for the Hopf Link in our tables is incorrect. The arc notation for L2a1{0} and L2a1{1} should read {{4,2},{3,1},{2,4},{1,3}} and {{4,2},{1,3},{2,4},{3,1}}, respectively.